联系我们

关于高压冷冻仪中液氮的热力学考虑

液氮的压缩和加热

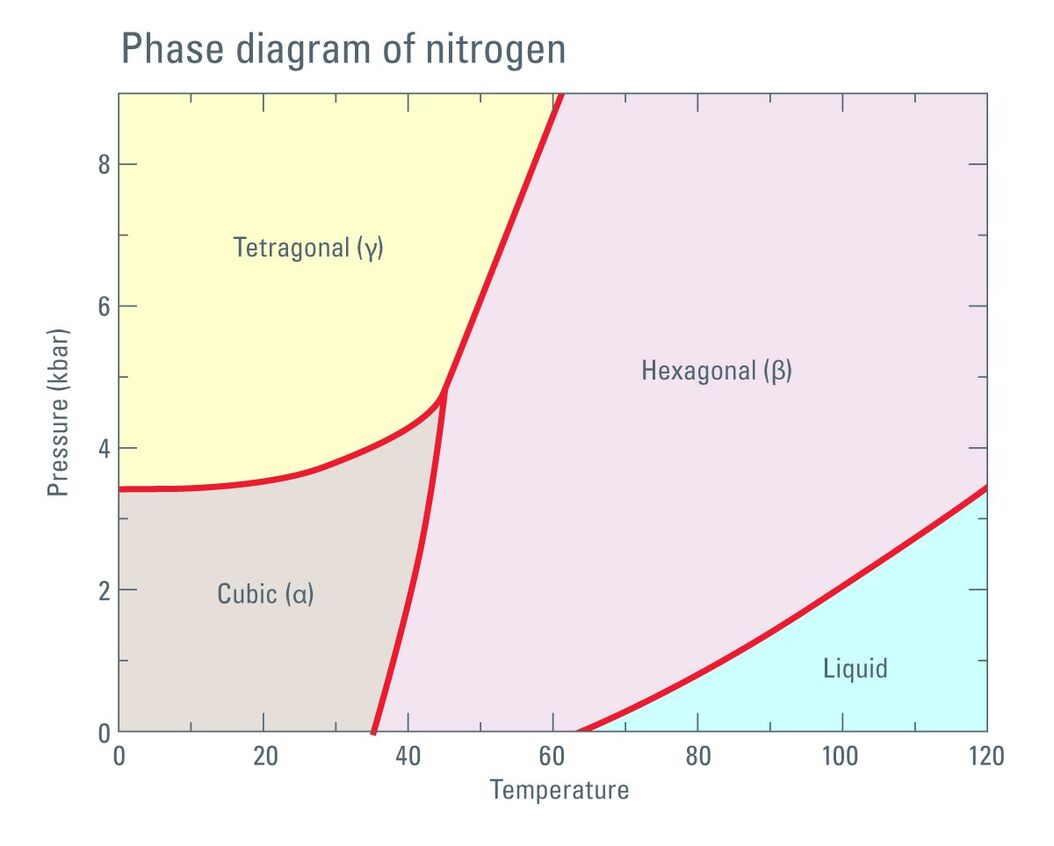
Figure-0_14.jpg

在高压冷冻过程中，待冷冻样品和冷却剂的相变导致我们对使用液氮作为冷冻剂提出一定的质疑。根据氮气的相图（图1），温度或压力的变化将改变该元素的状态。在环境压力下，氮气在-209.86℃至-195.80℃之间为液态。在有限的相位边界内，它是一个相当脆弱的平衡。

引入高压将不可避免地使影响液相的参数向一个方向或另一个方向移动。重要的问题是，该偏移是否会对引起相变，如果是，它是朝向固相还是液相。

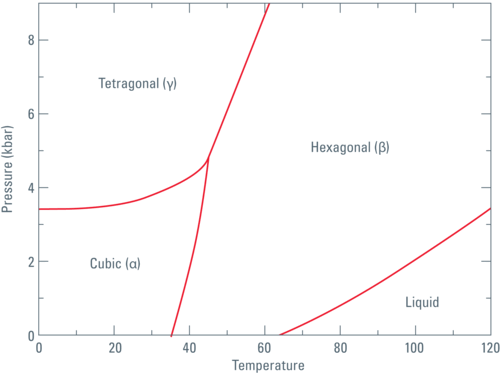
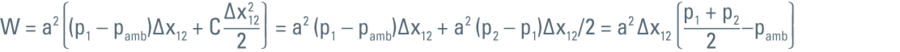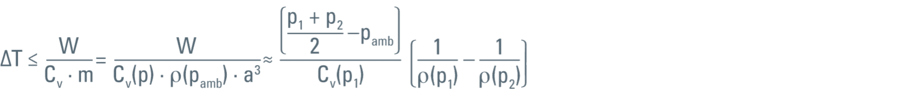Fig. 1: Phase diagram of Nitrogen according to Young DA: Phase Diagrams of the Elements; UCRL-51902 (1975).

LN2的压缩和温度变动

为了产生高压LN2喷射流，我们必须将液体压缩至特定体积。

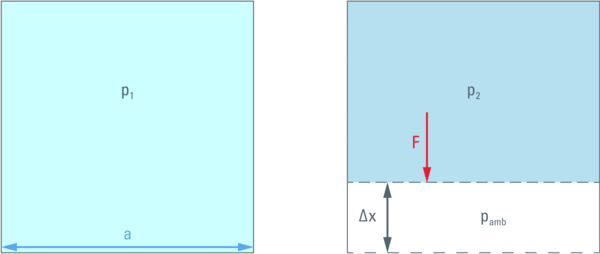
为了说明这一点，让我们考虑一个给定体积(a3)充满液体的立方体。可移动一壁（距离∆x），以压缩内部液体。这种压缩将在立方体内部(p)和外部(pamb = 1,013 bar)之间产生压差。

压缩定义为响应压力变化的相对体积变化： 

其中Δx12是压缩液体从压力p1到压力p2所需的壁的位移，V(p1)是p1时的液体体积。

另一方面，该压缩产生的压差乘以侧壁面积(a2)是作用于抵抗压缩的力(F)。

因此，将壁移动距离Δx需要能量F⋅ Δx.。

为了将液体从p1压缩到p2，壁必须通过一定的距离移动，这个移动是将液体从p1压缩到p2所做的功 (W)。

为了计算功(W)，我们使用了以下积分：

如果我们假设压缩遵循线性压缩定律 

则上述积分可转化为：

由于能量是系统做功的能力，因此上述公式中的功是最终将增加液体温度的能量（在这种特定情况下为LN2）：

其中Cν代表比热，ρ (p)代表压力(p)下LN2的密度。

当该公式应用于Jacobsen等人给出的数据集时。 [1]，事实证明，仅依靠压缩所做的功不足以将LN2加热到冰点以上。

在我们的计算中（对线性压缩定律适用的一系列压力部分进行），液体密度的直接压缩将使温度升高到约97 K。这意味着在200 mPa下做的功（或能量）将不足以保持LN2高于冰点的98.98K。

总结

在我们急于得出任何结论之前，我们必须考虑其他几个方面。97 K的温度非常接近冰点温度，因此我们预期只有10-20%的液氮被冷冻，因为相变过程中产生的熔解热将阻止进一步结晶。可能使温度升高到冰点以上的其他热量是摩擦和气泡压缩产生的热量。由于这些过程很可能是系统的一部分，因此应在LN2实际温度的最终估计中考虑这些过程。

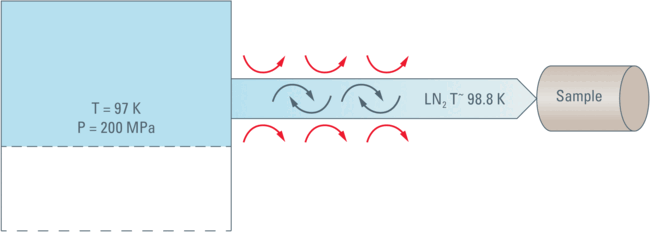
计算表明，LN2在压缩过程中升温，要么是过冷液体，要么是在200 mPa下有小部分固体夹杂物的液体。

如果实际形成了任何此类结晶夹杂物，当氮气被推向样品时，它们肯定会通过与管壁的接触以及移动过程中发生的湍流和摩擦而被加热至熔化。

所有这些都意味着氮气将以液态形式到达样品，最有可能在-174.17℃（或98.98 K，LN2的冰点）或略高的温度范围内。

在200 MPa压力下，不存在Leidenfrost现象，因此液氮与样品夹具的热接触非常好，并且通过热传导样品的热量能够很好地被LN2消散。

相关文章

想了解更多信息？
请咨询我们的专家。

价格

我需要配置或价格信息。

预约演示

我需要现场或远程演示。

服务与支持

我们能为您提供什么帮助？

应用支持

我需要专业帮助/培训来支持我运作机器。

您想获取专人咨询吗？ Show local contacts

Beckman Coulter LinkBeckman Coulter LogoGenedata LinkIDBS LogoIDBS LinkIDBS LogoAbcam Limited LinkAbcam Limited LogoMolecular Devices LinkMolecular Devices LogoPhenomenex LinkPhenomenex LogoSciex LinkSciex LogoAldevron LinkAldevron LogoIDT LinkIDT Logo
Scroll to top