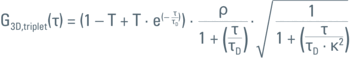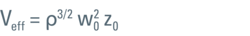![[Translate to chinese:] Sub-Femtolitre volume_Fluorescence correlation spectroscopy (FCS) Fluorescence_Correlation_Spectroscopy_FCS_sub-emtolitre_volume.jpg](/fileadmin/_processed_/f/4/csm_Fluorescence_Correlation_Spectroscopy_FCS_sub-emtolitre_volume_b55eea39aa.jpg "[Translate to chinese:] Sub-Femtolitre volume_Fluorescence correlation spectroscopy (FCS)")
FCS——方法论
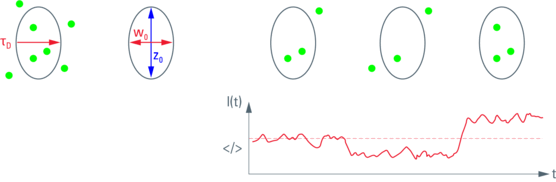
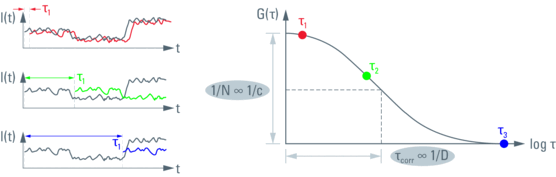
FCS 是一种光谱分析方法。在这种情况下，“比色皿”是一个衍射受限的光斑（图 1）。因此，使用显微镜的原因是要有一个高数值孔径镜头，将光束聚焦到飞升大小的光斑中。使用显微镜的一个额外的好处是可以拍摄样品的图像，用于参考和定位测量点（ROI）。在FCS中，主要的读出数据是随时间变化的荧光强度（荧光轨迹或强度轨迹）。荧光波动隐含地编码了粒子数量（即波动的幅度）和粒子停留时间（即波动的频率），见图 2。通过对这些数据进行自相关分析（“自相似性测试”）和曲线拟合，可以定量地获得这些参数（图3和图4）。在共焦光斑中，激发光和检测光的几何形状大致遵循三维正态分布。通过将其近似为高斯函数，可以找到FCS自相关函数的解析模型。其参数及其物理意义总结在表1中。
图 1（左）： 观测体积和重要参数。扩散时间 τD 表示分子在观测体积内停留的时间，即横向扩散所需的时间。观测体积的横向延伸（束腰）w0 和轴向延伸 z0 均已给出（右侧）。它们的比值 z0/w0 即为偏心率或结构参数 κ。
图 2（右）： 荧光强度轨迹。分子进出观测体积（上测）会导致荧光强度的随机波动。
图3（左）：自相关原理。荧光轨迹被复制，并与自身相乘，然后将结果相加。这个过程会重复多次，每次都将第二个数据集向右移动一个增量τi（延迟时间）。在小的延迟时间后，数据仍然保持自相似性，因此总和较大（红色）。较长的移动意味着较小的数（绿色和蓝色）。这种技术分析了分子通过观测体积扩散的频率的潜在信息。
图4（右）：将自相关函数G(τ)绘制成关于延迟时间t的图形。G(τi)代表不同的延迟时间，根据图3中的信息（红色、绿色和蓝色点）进行定性绘制。G(0)处的振幅编码了粒子数N的倒数。半最大振幅处的时间（拐点）给出了扩散时间τD，也称为相关时间。通过这些数值，结合适当的校准，可以获得浓度c和扩散系数D。
有关FCS曲线“解析”的详细信息，即在不同时间域内观察到哪些过程，以及该主题的全面介绍，请参阅Petra Schwille和Elke Haustein撰写的在线文章 [3]。
| 参数 | 名称 | 意义 |
|---|---|---|
| ρ | 当前振幅 | 由特定分子种类贡献的G(0)振幅 |
| τD | 扩散时间 | 分子在有效观测体积Veff内停留的时间 |
| τT | 三重态时间 | 分子在暗态中停留的时间 |
| T | 三重态比例 | 处于暗态的分子比例 |
| κ | 结构参数 | 有效观测体积Veff的偏心率κ |
表1：用于三维中单一分子种类和正常扩散数据拟合的三维高斯三重态模型参数。
校准—从相对数值到绝对数值
在FCS测量中，两个主要的关注参数是扩散时间τD和分子数N。它们分别与扩散系数D和浓度c直接相关。然而，τD和N都是相对数值，受到每台仪器和多个实验参数的影响。为了获得扩散系数D和浓度c的绝对数值，就需要进行仪器校准。
校准策略
文献中介绍了三种确定 Veff 的方法：
- 使用三维荧光珠测量共焦体积并拟合三维高斯函数。
- 制备浓度序列并绘制 N 与 c 的函数关系图。
- 测量已知 D 的已知染料，曲线拟合得出 τD 和 κ，由此计算 Veff。
每种方法都有其缺点和优点。例如，第一种方法能够精确描述共聚焦体积，并提供关于三维高斯近似准确性的详细信息。然而，它并不是在像实际测量那样的水溶液中进行的。第二种方法不依赖于任何模型，不对Veff的几何形状或扩散模型做任何假设。因此，它不包含关于其形状的信息，过程较为繁琐，并且在不使用曲线拟合来估计N的情况下可能会受到暗态的影响，但它适用于广泛的浓度范围。最后一种方法的工作条件与实际FCS测量非常接近，包含一些关于Veff几何形状的信息，并且易于实现。接下来，我们将逐步研究这一策略。如需对这三种方法进行详细比较，请参阅 [1]。
通过曲线拟合获得有效体积
由于这种方法基于曲线拟合，因此结果的质量在很大程度上取决于模型对实际情况的描述程度。其中最有力的假设是Veff具有三维高斯几何形状，这是FCS分析中常用的做法。然而，如果系统存在未对准情况，这一假设将被打破。此外，还需要自相关函数具有良好的信噪比，因为τD和κ都是从同一数据集的拟合中确定的。这最好通过在水溶液中使用浓度范围在 0.1 nM 至 10 nM [1] 之间的明亮且光稳定的染料来实现。有效体积可以如方程1所示给出。
公式 1：有效体积。与FCS测量相关的观测体积大小，其中w0为横向扩展，z0为轴向扩展。这两个参数取决于通过校准测量的曲线拟合获得的τD和κ。请注意，Veff通常比文献中通常提到的共聚焦体积大2^(3/2) ≈ 2.8倍。
参考文献
- Madge D, Elson E, Webb WW: Thermodynamic fluctuations in a reacting system – Measurement by fluorescence correlation spectroscopy. Phys. Rev. Lett. 29 (1972) 705–708
- Rigler R, Widengren J: Ultrasensitive detection of single molecules by fluorescence correlation spectroscopy. Bioscience 3 (1990) 180–183
![[Translate to chinese:] Sub-Femtolitre volume_Fluorescence correlation spectroscopy (FCS)](/fileadmin/_processed_/f/4/csm_Fluorescence_Correlation_Spectroscopy_FCS_sub-emtolitre_volume_ea78bcbb27.jpg "[Translate to chinese:] Sub-Femtolitre volume_Fluorescence correlation spectroscopy (FCS)")
